How do you find the drag coefficient of a ball?
The drag is given by the drag equation: D =.5 * Cd * r * A * Vt^2 where r is the gas density, Cd is the drag coefficient which characterizes the effects of shape of the ball, A is the cross-sectional area of the ball, and Vt is the terminal velocity. On the figure at the top, the density is expressed by the Greek symbol “rho”.
How does the drag coefficient influence the drag force?
The drag coefficient of an object in a moving fluid influence drag force. Any object moving through a fluid experiences drag - the net force in the direction of flow due to pressure and shear stress forces on the surface of the object. The drag force can be expressed as: Fd = cd 1/2 ρ v2 A (1) where. Fd = drag force (N)
What is the drag coefficient of a golf ball in wind tunnel?
The wind tunnel results for the commercial golf balls were consistent at higher Reynolds numbers, 8.0 × 10 4 and had a drag coefficient range of C D = 0.275 ± 0.0225 [ 4] . Larger variations occur at lower Reynolds numbers, <5.0 × 10 4, for the commercial golf balls.
Do golf balls drag coefficient vary with Reynolds numbers?
Introduction Six golf balls were tested in a wind tunnel and Star CCM+ was used to simulate how the golf balls drag coefficients, C D, varied with Reynolds numbers, Re D, in relation to the flow around the balls.

How do you calculate the drag coefficient of a ball?
0:338:42Demonstrating and Solving for Drag Coefficient - YouTubeYouTubeStart of suggested clipEnd of suggested clipWe get the drag coefficient equals the quantity. 2 times mass times acceleration due to gravity allMoreWe get the drag coefficient equals the quantity. 2 times mass times acceleration due to gravity all divided by the quantity. Density times cross sectional area times the terminal speed squared.
What is the drag force on a ball?
The drag force on an object moving through a fluid can play an important role in determining the motion of the object, especially if the object is moving at high speed. For example, the drag force on a baseball or a cricket ball is equal to the weight of the ball at a ball speed of about 40 m s−1.
What is the drag coefficient of a car equation?
The drag force is generally modeled as: D = 0.5•rho•V^2•S•Cd; where tho is the air density, V is basically the speed of the car, S is the frontal area of the car if we assume that the wake drag is dominant, and Cd is the parasitic drag coefficient.
How do you calculate Reynolds number on a golf ball?
The Reynolds number is defined as Re = VL/ν where V is the flow speed, L the ball size and ν is the viscosity coefficient. The transition from laminar to turbulent flow occurs at a critical value of Re which depends on details of the system, such as surface roughness.
What is the drag coefficient of a tennis ball?
Drag forces on tennis balls in flight were analysed by mounting tennis balls in a wind tunnel at wind speeds up to 66.6 ms−1 (150 mph). It was found that different brands of standard size tennis ball and a larger tennis ball had a drag coefficient of approximately 0.55.
What is the drag coefficient of a football?
0.18 to 0.20The average drag coefficient for American footballs is in the range of 0.18 to 0.20 when the major axis of the ball is pointed to the wind direction and 0.75 to 0.78 when the minor axis is pointed to the wind direction. The NCAA ball possesses slightly higher value of drag coefficient compared to the NFL ball.
How do you calculate lift and drag coefficient?
The lift coefficient is defined as: CL = L/qS , where L is the lift force, S the area of the wing and q = (rU2/2) is the dynamic pressure with r the air density and U the airspeed. Similarly, the drag coefficient is written as: CD = D/qS , where D is the drag force and the other symbols have the same meaning.
How do you calculate drag coefficient using Reynolds number?
Figure 1 graphs the dependence of drag coefficient for a sphere and a cylinder in crossflow on the Reynolds Number Re = ρuD/η, where D is the sphere (cylinder) diameter, η the viscosity of liquid, and .
Is drag coefficient constant?
The drag coefficient is directly influenced by the velocity of the flow of the object in the fluid. If the velocity is kept constant over a period, there may be a change in the drag, but the drag coefficient is constant as it is the dimensionless quantity.
How does the Bernoulli principle affect a golf ball?
Backspin generates lift by disturbing the airflow around the ball. Backspin is created by the angled edge of the clubface and helps create more lift by speeding up the air going over the top of the ball and slowing down the air flowing underneath the ball. This is known as Bernoulli's principle.
How do Newton's laws apply to golf?
The impact between a club and the ball produces equal and opposite forces, demonstrating Newton's Third Law of Motion, and also transfers momentum from the club to the ball. "Science of Golf" is produced in partnership with the United States Golf Association and Chevron.
What is Reynolds number example?
Reynolds Number Example Problems Problem 1- Calculate Reynolds number, if a fluid having viscosity of 0.4 Ns/m2 and relative density of 900 Kg/m3 through a pipe of 20 mm with a velocity of 2.5 m. From the above answer, we observe that the Reynolds number value is less than 2000.
What is the drag coefficient?
Drag coefficient. ) is a dimensionless quantity that is used to quantify the drag or resistance of an object in a fluid environment, such as air or water. It is used in the drag equation in which a lower drag coefficient indicates the object will have less aerodynamic or hydrodynamic drag.
What is drag in fluid dynamics?
Drag, in the context of fluid dynamics, refers to forces that act on a solid object in the direction of the relative flow velocity (note that the diagram below shows the drag in the opposite direction to the flow). The aerodynamic forces on a body come primarily from differences in pressure and viscous shearing stresses. Thereby, the drag force on a body could be divided into two components, namely frictional drag (viscous drag) and pressure drag (form drag). The net drag force could be decomposed as follows:
The drag coefficient quantifies the drag or resistance of an object in a fluid environment
Any object moving through a fluid experiences drag - the net force in the direction of flow due to pressure and shear stress forces on the surface of the object.
Example - Air Resistance Force acting on a Normal Car
The force required to overcome air resistance for a normal family car with drag coefficient 0.29 and frontal area 2 m2 in 90 km/h can be calculated as:
How is the aerodynamics of a ball determined?
The aerodynamics of a ball are determined by its mass and shape, in particular the nature of the surface. A complex pattern of dimples of varying sizes, shapes and depths influence the air flow around the ball. By roughening the surface, the critical Reynolds number is reduced to speeds within the golfer’s range.
What is the effect of air passing over the top of the ball on the ball?
This results – by way of Bernoulli’s principle – in lower pressure above and an upward force on the ball. Lift allows golfers to achieve greater distances. The character of fluid flow depends on a dimensionless quantity, the Reynolds number.
What is the drag crisis?
In 1912, Gustave Eiffel – of Eiffel Tower fame – made a remarkable discovery, known as the drag crisis. Studying flow around a smooth sphere, he found a drop in the drag force as the flow speed increased above a critical Reynolds number. The drag crisis extends the range of a rapidly travelling ball, but a smooth ball needs speeds in excess ...
What was the name of the discovery that led to the drop in drag force?
In 1912, Gustave Eiffel – of Eiffel Tower fame – made a remarkable discovery, known as the drag crisis. Studying flow around a smooth sphere, he found a drop in the drag force as the flow speed increased above Reynolds number 200 000 and continued to drop until about Re = 300 000 (see figure above).
What determines the character of fluid flow?
The character of fluid flow depends on a dimensionless quantity, the Reynolds number. Named for Belfast-born scientist Osborne Reynolds, it determines whether the flow is laminar (smooth) or turbulent (rough). Normally the drag force increases with speed.
How fast can a pro golfer drive?
The golfer controls the direction and spin of the ball by variations in his swing. A pro can swing his driver at up to 200 km/h, driving the ball 50% faster than this as it leaves the tee, on a trajectory about 10º above the horizon.
How many dimples are in a golf ball?
Most balls have about 300 dimples. Manufacturers promise greater control, stability and velocity on longer shots. Hundreds of dimple patterns have been devised and patented but the optimal design remains a challenge.
What is drag coefficient?
The drag coefficient is a number that aerodynamicists use to model all of the complex dependencies of drag on shape, inclination, and some flow conditions. This equation is simply a rearrangement of the drag equation where we solve for the drag coefficient in terms of the other variables.
What causes drag on the wing tips?
This additional source of drag is called the induced drag and it is produced at the wing tips due to aircraft lift. Because of pressure differences above and below the wing, the air on the bottom of the wing is drawn onto the top near the wing tips. This creates a swirling flow which changes the effective angle of attack along ...
Vertical Location
At launch the ball is inclined at some angle to the vertical, so we resolve the initial velocity into a vertical and horizontal component. Unlike the ballistic flight equations, the horizontal equation includes the action of aerodynamic drag on the ball.
Vertical Descent
During the vertical descent, for a light object, the weight and drag of an object are equal and opposite. There is no net force acting on the ball and the vertical acceleration is zero.
Velocity
The gas density has different surface values on the Earth and on Mars and varies with altitude. On the Moon the gas density is zero. Combining the last three equations, we can determine the terminal velocity:
Vertical Ascent
This is the equation for the velocity at any time during the vertical ascent. At the top of the trajectory, the velocity is zero. We can solve the velocity equation to determine the time when this occurs:
Horizontal Location
The horizontal equations are a little easier, since the only net force acting on the ball is the drag:

Overview
In fluid dynamics, the drag coefficient (commonly denoted as: , or ) is a dimensionless quantity that is used to quantify the drag or resistance of an object in a fluid environment, such as air or water. It is used in the drag equation in which a lower drag coefficient indicates the object will have less aerodynamic or hydrodynamic drag. The drag coefficient is always associated with a particula…
Definition
The drag coefficient is defined as
where:
• is the drag force, which is by definition the force component in the direction of the flow velocity;
• is the mass density of the fluid;
Background
The drag equation
is essentially a statement that the drag force on any object is proportional to the density of the fluid and proportional to the square of the relative flow speed between the object and the fluid.
is not a constant but varies as a function of flow speed, flow direction, object p…
The drag equation
is essentially a statement that the drag force on any object is proportional to the density of the fluid and proportional to the square of the relative flow speed between the object and the fluid.
is not a constant but varies as a function of flow speed, flow direction, object p…
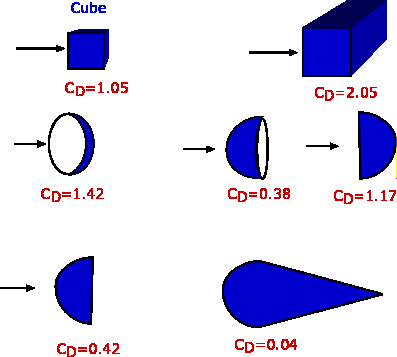
Drag coefficient examples
In general, is not an absolute constant for a given body shape. It varies with the speed of airflow (or more generally with Reynolds number ). A smooth sphere, for example, has a that varies from high values for laminar flow to 0.47 for turbulent flow. Although the drag coefficient decreases with increasing , the drag force increases.
As noted above, aircraft use their wing area as the reference area when computing , while autom…
Blunt and streamlined body flows
The force between a fluid and a body, when there is relative motion, can only be transmitted by normal pressure and tangential friction stresses. So, for the whole body, the drag part of the force, which is in-line with the approaching fluid motion, is composed of frictional drag (viscous drag) and pressure drag (form drag). The total drag and component drag forces can be related as follows:
See also
• Automotive aerodynamics
• Automobile drag coefficient
• Ballistic coefficient
• Drag crisis
• Zero-lift drag coefficient